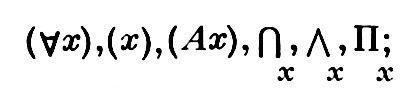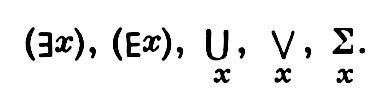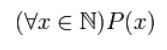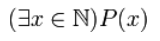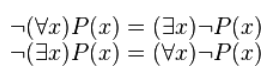Квантор двоеточие что обозначает
Vacuous truth и кванторы
ValueError: The truth value of an array with more than one element is ambiguous
Помогите с кодом, если будет возможно или объясните, что не так, точнее как можно исправить. В.
Предикаты и кванторы
Помогите решить. P(x, y) := (х – 1)(х – 2) + 3х = у

записать кванторами математическое определение: натуральное число m является простым если оно не.
Никак не получить. Вы не правильно поняли связи.
Сначала постулируется, что из ложи следует всё, что угодно, т.е. доказуемо для любого A.
Подскажите, а вот двоеточие что обозначает? В исчислении предикатов нет же никакого двоеточия? Пишут, что символ просто помогает сократить фразу ‘такой что’. Но в исчислении предикатов нет понятия ‘такой что’.
Добавлено через 39 минут
Что такое исчисление предикатов? Если ограничиваемся только языком, то формула может быть или предикатом, или конъюнкцие, или диъюнкцией, или отрицанием, или импликацией, или квантор-буква-формула. Скобки, точки и т.п. расставляются для удобства записи и чтения и нужны только лишь затем, чтобы однозначно «парсить» запись. Я, например, иногда пишу квантор-буква-(-формула-), а иногда квантор-буква-точка-формула, а иногда вместо точки двоеточие ставлю. А некоторые предпочитают запись (-квантор-буква-)-формула. Дело вкуса.
Авторские задачи на кванторы и предикаты
Всем доброго времени суток! Недавно от нашего преподавателя поступило задание: написать 5 авторских.
Перед следующими предикатами поставьте соответствующие кванторы
4. Перед следующими предикатами поставьте соответствующие кванторы так, чтобы получились.

Здравствуйте! Читаю книгу Хаггарти по дискретной математике.Помогите, пожалуйста, разобраться с.
MT1102: Линейная алгебра (введение в математику)
В алгебре высказываний применяют логические знаки для записи различных утверждений. Однако нам не достаточно этих знаков для выражения мысли типа «Всякий элемент %%x%% из множества %%D%% обладает свойством %%P(x)%%».
Понятие кванторов
Введем новые логические знаки, обозначаемые %%\forall%%, %%\exists%% и %%\exists!%%. Знак %%\forall%% называется квантором всеобщности, знак %%\exists%% — квантором существования, а %%\exists!%% — квантором существования и единственности.
Пусть %%P(x)%% — одноместный предикат, определенный на множестве %%D%%.
Квантор всеобщности
Используя квантор всеобщности, можно составить следующее высказывание
Читается как: «для любого %%x%% выполняется %%P(x)%%»; «для всякого %%x
P(x)%%»; «для всякого %%x%% верно %%P(x)%%» и т.п.
Пусть %%P(x)%% предикат %%x^2 \geq 0%%, определенный на множестве действительных чисел %%D = \mathbb R %%. Тогда высказывание %%\forall x
P(x)%% имеет вид %%\forall x
x^2 \geq 0%%. Это истинное высказывание, так как для любого значения пременной %%x = a \in \mathbb R %% получаем истинное высказывание %%a^2 \geq 0%%. Однако, высказывание %%\forall x
x^2 > 0%% ложно, например, как при %%x = 0%% получаем ложное высказывание %%0 > 0%%.
Квантор существования
Используя квантор существования, можно составить следующее высказывание
Читается как: «существует %%x%% такой, что %%P(x)%%»; «существует %%x%% с условием %%P(x)%%» и т.п.
Квантор существования и единственности
Используя квантор существования и единственности, можно составить следующее высказывание
Читается как: «существует единственный %%x%% такой, что %%P(x)%%»; «существует единственный %%x%% с условием %%P(x)%%» и т.п.
Отрицание «кванторов»
Докажем первое из них. Пусть высказываине %%\overline<\forall x
P(x)>%% истинно. Тогда высказывание %%\forall x
P(x)%% ложно. Поэтому для некоторого %%x = a%% имеем %%P(a)%% ложно. Тогда %%\overline
\overline
Аналогично доказывается второе утверждение.
Применение одного из кванторов «понижает» степень предиката на единицу. Из двуместного предиката получается одноместный предикат, а из одноместного — предикат %%0%% степени или высказывание.
Правила перестановки кванторов
P(x,y) \equiv \exists y
P(x,y) \equiv \forall y
Однако, разноименные кванторы переставлять местами нельзя. Рассмотрим двуместный предикат %%P(x, y): x + y = 0%%, определенный на множестве %%\mathbb R%%. Тогда высказывание %%\exists x
x + y = 0%% можно прочитать так: «существует %%x%%, которое в сумме с любым %%y%% равно 0». Это ложно высказывание.
Переставим разноименные кванторы местами и получим высказывание %%\forall y
x+ y = 0%%, которое можно прочитать так: «для любого %%y%% существует %%x%% такой, что их сумма равна 0». Это истинное высказывание. В итоге получили различные истинностные значения высказываний.
Для записи одноименных кванторов существуют следующие сокращения:
\forall y \equiv \forall x, y
\exists y \equiv \exists x, y. \end
Кванторы и символы математической логики
Собственность как правоотношение. Проблема понимания содержания права собственности и формы собственности.
Существует множество противоречий:
Со времен Рима существует две позиции:
1. В вещном праве реализуется субъектно – объектные отношения – отношения лица к вещи.
2. Реализует субъетно-субъектные отношения.(Шершеневич, Муромцев, Чичерин и др.)
Вещное и обязательственное право соотносятся как статика и динамика (Суханов).
Вещное и обязательное право (Коркунов): Вещное реализуется своими действиями, в обязательственном праве – действиями обязанных лиц.
Признаки вещного права:
1.Вещные права – по сути абсолютные правоотношения (определена одна сторона);
2.Существует непосредственное отношение лица к вещи, удовлетворение интересов лица с помощью вещи.
3.Бессрочный характер вещных прав.
4.Преимущественная защита вещных прав (Суханов)
5.Индивидуализированность: имущество как вещь.
6.Существует право следования, когда собственник меняется, а право сохраняется (например сервитут).
7.Специальные вещно-правовые способы защиты.
1.Абсолютные правоотношения – это странная конструкция, один приобрел – все обязаны, они его не знают. Такая конструкция может быть только в сознании юриста. Эта идея неконструктивна, в ней нет содержания правоотношения, эти отношения аморфны. По содержанию нам сказать нечего. Чем заменить? Интерпретировать иначе – как относительные отношения – не отношения лица с другими лицами, а с государством – публично-правовые отношения по поводу признания укрепления, защиты права. Это:
*объясняется возникновением их из закона, а не из договора.
*государство определяет условия этого (налоги, требования).
Появляются законные основания – реальное содержание этих отношений. «Право из неоткуда» исчезает. Не обсуждается проблема – в центре частного права стоит публично-правовой институт.
2.И.Кант. Гегель: неправовая трактовка, так как это не правовые отношения вообще, поскольку нет правовых оснований. Что есть вещное право? По Канту это отношения лица к лицу по поводу вещи, следовательно относительный характер отношений.
И.Кант: внутренне отношение человека к вещи – это не предмет правового регулирования. (Архипов с ним согласен).
3. Бессрочный характер правовых отношений. Право оперативного управления и хозяйственного ведения, сервитут устанавливаются на основе договора (обязательственное право). А где граница обязательственного и вещного права Вещное право возникает только после государственной регистрации. После этого возникает ситуация публичной власти. Наряду с обязательственным правом возникает вещное. Таким образом теоретическая конструкция вещного права несостоятельна.
4. Преимущественная правовая защита. В законодательстве – преимущество у обязательственного права. Способы защиты носят носят формальный характер. Могут быть применены к обязательственным правам. Для родового имущества виндикация невозможна. Т.о. вещное право как субъктно-объктные отношения несостоятельны, может быть субъектно-субъектная связь.
5. Очень часто на праве собственности имеется родовое имущество. Объект может быть как индивидуализирован, так и нет. Выделяют для того, чтобы произвести виндикацию. (Архипов считает это спорным)
6. и 7. Это формально. Не вытекает их вещно-правовых способов защиты. Например, арендатор может быть виндикатором, даже в отношении собственника, следовательно используются как в вещном, так и в обязательственном праве. Иногда неприменимы (родовое имущество.)
Господство лица над вещью – это не право, так как это субъктно-объектные отношения.
Отличия отношений собственности.
С одной стороны неограниченность господства лица над вещью. Собственность неограниченный ограничитель, так как закон-основание, следовательно правовой характер.
Триада собственника (глоссаторы): может передать любое правомочие, оставаясь собственником, следовательно отношения к собственности не имеется. Это не содержание права собственности. Идея триады соответствует средневековому типу сознания.
Венедиктов предлагал четвертый элемент – использование(вполне самостоятельный элемент). Многие отвергли.
На практике абстрактные правоотношения индивидуализированы. Реальное содержание в законе, а мы не отказываемся. Эти отношения не цивилистические, а комплексные.
Наиболее корректен Гегель, так как собственность – продолжение лица, поскольку он вкладывает свою волю. С точки зрения воли, вложенная в вещь воля – продолжение субъекта. Покушение на вещь – есть покушение на собственника.
Момент присвоения. Гегель рассматривает отношения лица к вещи как к своей. Кант говорил о субъект-субъектных отношениях. (Архипов считает, что оба правы, таким образом отношения двуедины: объект-субъектные, субъект-субъектные).
Дополнительная литература по другим вопросам.
Проблемы юридической ответственности. Липинский.
Правосознание. Ильин. Работа о сущности правосознания.
Злоупотребление правом. Малиновский.
Юридическая практика. Леушин.
Проблемы общей теории права и государства. Нерсесянц.
В английском языке ври ведении электронной переписки широко используются различные сокращения, произношение которых сходно с произношением некоторых слов. Некоторые примеры таких сокращений приведены в таблице:
| Написание | Произношение | Перевод |
| B | be | быть, находиться |
| ate | «есть» в past simple | |
| for | для | |
| C | see | видеть |
| R | are | есть, является |
| too | очень, слишком | |
| U | you | ты, вы |
| Y | why | почему |
| activ8 | activate | активировать |
| gr8 | grate | отлично, великолепно |
| m8 | mate | товарищ |
| h8 | hate | ненавидеть |
| l8r | later | позже |
| 2day | today | сегодня |
| NE1 | anyone | кто-нибудь |
| w8 | wait | ждать |
| 4eva | forever | навсегда |
| b4 | before | перед, до |
| there4 | therefore | поэтому |
В различных областях математики, а также во многих других точных науках для сокращения записи выражений также используются специальные символы, считающиеся международными и понимаемые ученые из разных стран. Применение данных символов позволяет компактно записывать формулировки теорем, определений и других математических утверждений.
Рассмотрим наиболее широко применяемые символы.
Символ «»» эквивалентен фразе «для любого», «для произвольного», «для какого бы то ни было», «для всех». Данный символ имеет собственное название: квантор общности.
Символ «$» обозначает «существует», «найдется» (от англ. exists). Данный символ имеет собственное название: квантор существования.
Запись «$!» означает «существует, и притом единственный» и называется квантором существования и единственности.
Символ « \ » обозначает «без», «за исключением».
Символ « | » обозначает «такой, что», «который», «где». Эквивалентом данного символа является символ двоеточия «:».
Символ «Ù» обозначает «и».
Символ «Ú» обозначает «или».
Символ «Ø» обозначает «не».
Символ «º» обозначает «эквивалентно», «то же самое, что и…»
Если некоторое свойство (1) влечет за собой свойство (2), то записывают (1)Þ(2). Когда эти два свойства равносильны, пишут (1)Û(2). Вместо «Þ» иногда используют символ «®».
Примеры выражений с использованием рассмотренных математических символов:
$ x : x 2 +1=0 (ложное высказывание)
$ x : 2 x 10 : x 2 =3 x : 0 ³1 x : x 2 –1=0 (существует как минимум один…)
$x,y : x=-y Ù x 2 >y Ù x 0 (верно ли оно?)
Ø»x>y : x 2 >y 2 (выполняется, например, для x=5 и y=-10)
«DABC : ÐABC+ÐBCA+ÐCAB=180 o
Ø$DABC : ÐABC+ÐBCA+ÐCAB¹180 o
Лекция 1
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
КВАНТОР
Полезное
Смотреть что такое «КВАНТОР» в других словарях:
квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика
КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия
Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания
квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник
квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas
Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия
квантор — кв антор, а … Русский орфографический словарь
Предикаты и кванторы
Вы будете перенаправлены на Автор24
Понятие предиката
Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.
Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:
Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:
Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.
Примеры предикатов
Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.
Готовые работы на аналогичную тему
Операции над предикатами
Рассмотрим применение операций алгебры логики к предикатам.
Логические операции:
Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.
Кванторы
Чаще всего используют кванторы:
В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.
Примеры применения кванторов
С помощью квантора всеобщности можно записать следующие ложные высказывания:
который будет иметь вид:
Для записи истинных высказываний используем квантор существования:
Запись будет иметь вид:
Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.
Операции над кванторами
Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
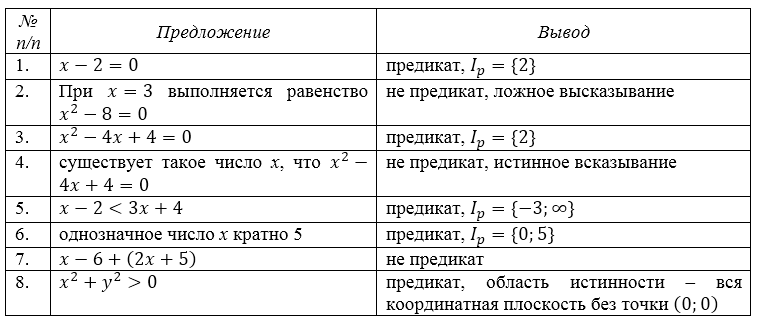
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 07 04 2016